UVA DETECTOR
Data and application notes


PURPOSE

The SolData UVA detector is designed to measure ultraviolet radiation within the 315-400 nanometer (nm) spectral range. The detector uses a narrow band interference filter to select 365 nm UVA with a bandwidth of about 10 nm. The UVA detector can be used to measure the direct solar spectral irradiance at 365 nanometers as well as the spectral irradiance from other sources such a halogen lamps, fluorescent lights and solarium lamps. Used with a UVA Lamp light source, UVA transmittivities and reflectivities of various materials can also be measured. A UVA Demo Set with a selection of filters and fluorescent and phosforescent materials is available for use in science education.

DESCRIPTION

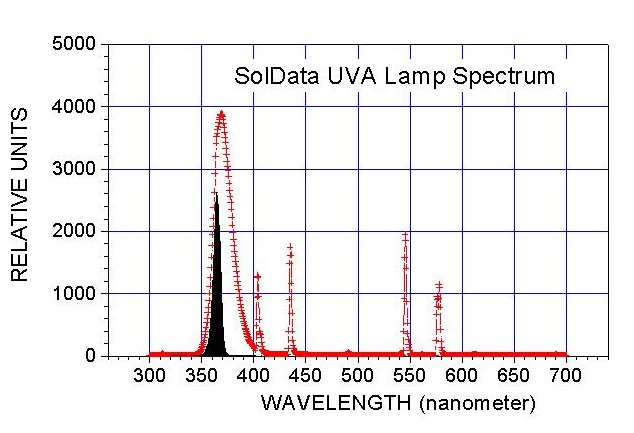
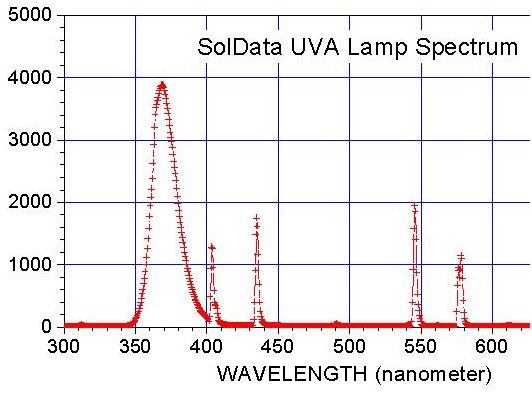
SPECTRAL RESPONSIVITY

The spectral responsivity of the UVA instrument is primarily determined by the transmittivity of the interference filter. The figure at the right shows the measured transmittivity for a typical SolData instrument. The off peak rejection of radiation is in excess of 106. To test this property expose the radiometer to a strong UVA source such as direct sunlight. Cover the aperture with a high pass filter cutting off all radiation below 400 nanometers but with high transmittance above 400 nm. The instrument output should fall to zero, confirming that off peak radiation is not being measured.


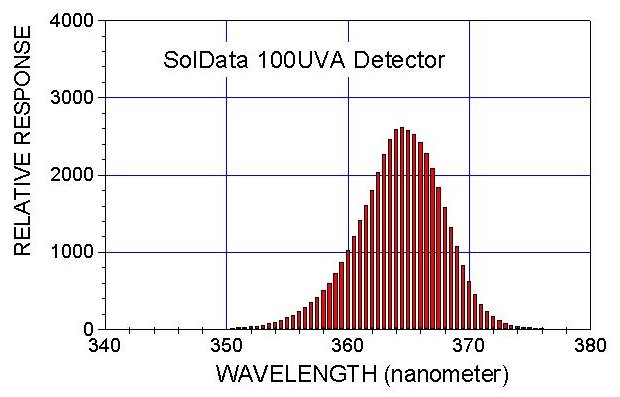
UVA Detector Spectral Response

The SolData UVA detector uses a Hamamatsu silicon photodiode and a narrow band filter. Used with a solar tracker and data logger direct solar irradiance data can be collected.

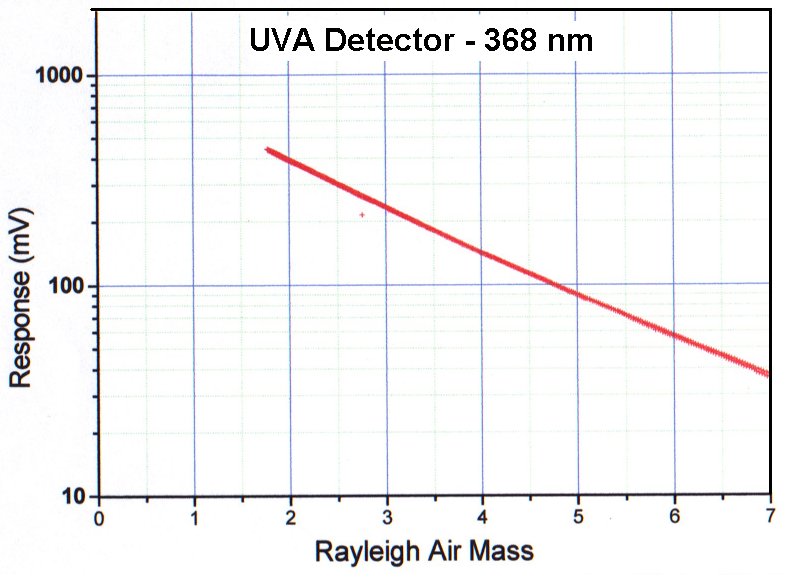
This solar irradiance data at 368 nm is from 25 July 1999 in northern Greenland (76.5 N). The Langley plot shown here can be extrapolated to outside the atmosphere (to air mass zero) for calibration against known extraterrestrial solar irradiance spectra.

TECHNICAL SPECIFICATIONS
Mass:110 gram
Diameter:25 mm
Length:100 mm
Cable:120 cm, 5 pole DIN
Detector:Hamamatsu (Si)
Spectral response:360-370 nm
Spatial response:Directional
Supply voltage:5-12 V DC (< 1 mA)
Output voltage:1 volt/10 µW/(cm2•nm)

Click here for UVA units of measurement.

INTERFACE OPTIONS
Use a SolData battery box (type 102DBX) and a standard digital voltmeter as your readout.
The 5 pole DIN connector is compatible with the widely used PASCO Science Workshop ®.

5 POLE DIN CONNECTOR PIN CONNECTIONS
PIN (1)Signal out
PIN (4)+5V to 12V supply
PIN (5)Ground
With this information you can connect the detector directly to your own data collection system.


UVA EXPERIMENTS


How much UVA is transmitted by glass, UV-film, plexiglas and other materials? Insert the material under test between the UVA lamp and the detector. Check your eyeglasses for UVA transmittivity!

The UVA detector responsivity (black graph) matches the major emission peak near 370 nm from the SolData UVA lamp (red graph).


ACCESSORIES


Use the 102DBX battery box and a standard digital voltmeter as your data readout device. The unit is compatible with the SolData Lux Detector and the UVB Detector as well.

Bias box type 102DBX. The input connector is a male 5 pole DIN connector. The output goes to 4 mm safety jacks suitable for a standard voltmeter. The unit requires a 9 V block battery (supplied).

The UVA Lamp is a useful accessory when using the UVA Detector. The spectral irradiance at a distance of 30 cm in front of the lamp is about 10 µW/(cm2• nm). Supply voltage: 220 VAC. Size: 8 x 8 x 19 cm. Mass: 1 kg.

The UVA Lamp spectrum is a good match to the UVA detector response curve. The low pressure mercury vapor spectrum from the lamp has a major peak around 370 nanometers.


UVA UNITS OF MEASUREMENT

The UVA detector output signal U is proportional to the spectral irradiance of the incident radiation at 365 nm (bandwidth 10 nm). As the device will most often be used to perform physical or radiometric measurements, it is calibrated in µW/(cm2 • nm). To illustrate these units the following figure shows the spectral irradiance of solar radiation at "air mass zero", i.e. outside the earth's atmosphere. The spectrum has been measured from satellites and has been published by NASA.

Note that the total area under the graph equals the "solar constant", ca. 1367 W/m2. You can make a rough estimate to check this as follows: The graph is roughly shaped like a triangle with a base width of about 1500 nm and a height of about 180 µW/(cm2 • nm). The area of the triangle is: 1/2 • 1500 nm • 180 µW/(cm2 • nm) = 1.35 • 105 µW/cm2 = 0.135 W/cm2 = 1350 W/m2, which is reasonably close to the value of the solar constant.

The spectrum of direct solar irradiance is of course modified during passage through the atmosphere due to Rayleigh scattering and molecular absorption. The UVA Detector can be used, among other things, to study such phenomena. On a clear day Rayleigh scattering is the primary factor causing attenuation of the UVA irradiance.

Wavelength: 310 nm 330 nm 340 nm 350 nm 365 nm 380 nm 405 nm
Air Mass: 0 68.9 105.9 107.4 109.3 113.2 112.0 164.4
Air Mass: 1.5 6.2 18.8 29.8 34.3 43.2 48.9 82.4
The table shows values for the spectral irradiance in µW/(cm2 • nm) measured for air mass zero (NASA, Thekaekara, Solar Energy 14, pp 109-127) and for air mass 1.5 (Bird & Hulstrom, Solar Energy 30, no. 6, pp 563-573, 1982). NB: The strong attenuation at 310 and 330 nm is due to the Huggins ozone absorption band. The air mass 1.5 data corresponds to a solar elevation angle of about 42 °

EXAMPLE:

 You have measured the direct solar irradiance at 365 nm for a range of solar elevation angles during a clear, sunny day. The values you obtain U will be in volts and will be very low early and late in the day and rather high around noon. Draw a graph of these results as a function of the air mass through which the direct rays of the sun have passed. For elevation angles V above about 30 ° you can approximate this by: AM = 1/sin(V). The results should be plotted in a semi-log coordinate system with U on the vertical log axis and AM on the horizontal axis. You can see an example of such a graph, called a Langley plot, in the Description section above.

Extrapolate your graph back to air mass zero, and read off the voltage value on the logarithmic U axis. Suppose that the value which you read is 12 volts. This voltage would correspond to the extraterrestrial solar irradiance at 365 nm. From the table above you can see that this value (at the mean earth-sun distance) is 113.2 µW/(cm2 • nm). You can therefore conclude that your instrument sensitivity is 113.2/12 = 9.4 µW/(cm2 • nm) per volt.

This valuable piece of information can later be used to evaluate the 365 nm UVA emission from other "down to earth" UV sources such as halogen lamps, fluorescent lamps and solarium lamps.


E-mail to SolData...

TOP OF THIS PAGE